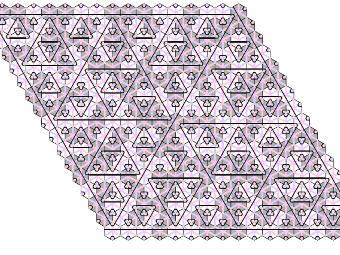
Фрагмент непериодического замощения. Иллюстрация авторов исследования
Австралийские математики Джошуа Соколар и Джоан Тэйлор решили задачу одной плитки (einstein problem - не путать с Einstein's problem). Статья ученых еще не принята к публикации, однако ее препринт доступен на сайте arXiv.org.
Замощением плоскости называется представление ее в виде набора
склеенных по границам фигур (называемых плитками). Один из простейших
примеров - так называемое гексагональное замощение,
когда плоскость, как соты, составлена из шестиугольников, соединенных
по сторонам. Замощение называется периодическим, если при сдвиге на
некоторый вектор оно переходит в себя. В гексагональном случае это,
например, вектор, соединяющий центры соседних шестиугольных ячеек.
В рамках новой работы ученые решали проблему построения
непериодического замощения при помощи всего одной плитки (это и есть
задача одной плитки). Форма полученной ячейки, как и в предыдущем
случае, шестиугольная, однако благодаря особой раскраске замощение
получается непериодическим. Помимо двумерной задачи, исследователи
предложили трехмерный аналог своего результата.
Помимо практических приложений (например, в кристаллографии)
теория замощений является источником вдохновения для художников.
Например, нидерландский художник Мауриц Эшер создавал целые картины с
использованием необычных замощений. В основе его "Восьми голов", в частности, лежит прямоугольное замощение.
Источник: Лента.ру
|